Thermocline in packed bed thermal energy storage systems

Previous essays have detailed the energy equation for packed beds:

$$(\epsilon_b \rho_f C_{p,f} + (1 - \epsilon_b) \rho_s C_{p,s}) \frac{\partial{T}}{\partial{t}} = \frac{\partial}{\partial{z}}(\lambda \frac{\partial{T_f}}{\partial{z}}) - \rho_f C_{p,f} u \frac{\partial{T}}{\partial{z}} - \frac{4h_w}{d_i}(T_f - T_w) + S_e$$

Solving the above equation under certain boundary and initial conditions leads to the formation of a thermocline within the packed bed. The thermocline refers to the transition zone between a hot and cold region, as shown below:

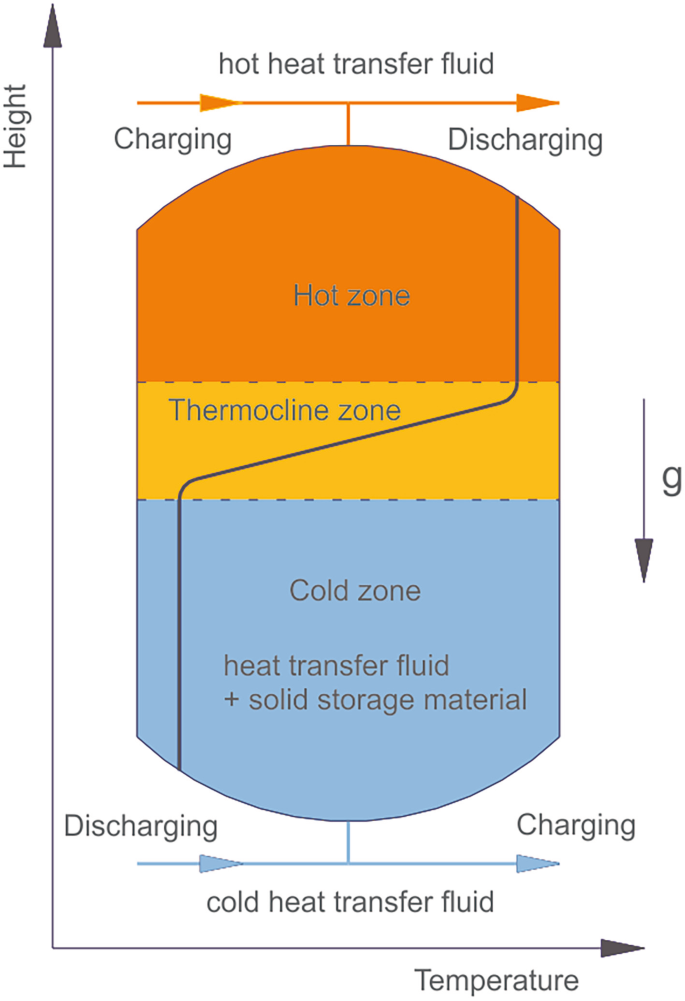
Also called the thermal front, its shape and size depend, in part, on the effective thermal conductivity of the bed. Over a long enough period, the hot and cold regions would equalise. This spreading of the thermal front is undesirable and reduces the energy recovery efficiency.

In an ideal packed bed thermal energy storage system, the effective thermal conductivity would be 0, and the thermocline would be a sharp front. In this case, during idle periods, there would be no mixing of the hot and cold ends. We can therefore conclude that there is an advantage to longer packed beds where the thermal front occupies a smaller fraction of the total bed length. However, longer beds will increase pressure drop and blower/pump energy demand.

In systems where the working fluid is a gas, the densities of the hot and cold fluids can vary significantly, resulting in a stratified fluid. As a result, the cold (dense) fluid phase must enter at the bottom of the vessel, with the hot end at the top. If the system were flipped, with the cold fluid flowing in a downwards direction, the thermocline would broaden. In systems where the temperature difference between the hot and cold ends causes a significant difference in density, the spreading of the thermal front is accelerated.

To capture this effect, it is important to include the bouyancy terms in the momentum balance equation.