Thermal gradients in particles

In previous essays, we discussed the local thermal equilibrium model, which assumes that the fluid and solid are in thermal equilibrium at the same temperature. In reality, there exists a thin thermal boundary layer between the solid and fluid, which, if thick enough, can cause a difference in their temperature. The rate of heat transfer through this layer is determined by the heat transfer coefficient, $h_{fs}$.

In addition to this thermal gradient between the particle and fluid, there will also be a thermal gradient within the particle itself. In almost all practical applications involving heat transfer within a packed bed, it can be assumed that the temperature within the solid particles remains constant. However, that is not always the case, and it will depend on the Biot number, defined as the ratio of the thermal resistance for conduction inside a body to the resistance for convection at the surface of the body. For a particle in a packed bed:

$$Bi = \frac{h_{fs}r_p}{k_s}$$

Where $r_p$ is the particle radius, and $k_s$ is the solid thermal conductivity. For high Bi numbers > 1, the thermal resistance dominates, and as a result, large temperature gradients emerge. For low Bi numbers < 1, the convective heat transfer resistance at the surface dominates, leading to an almost uniform temperature profile within the solid.

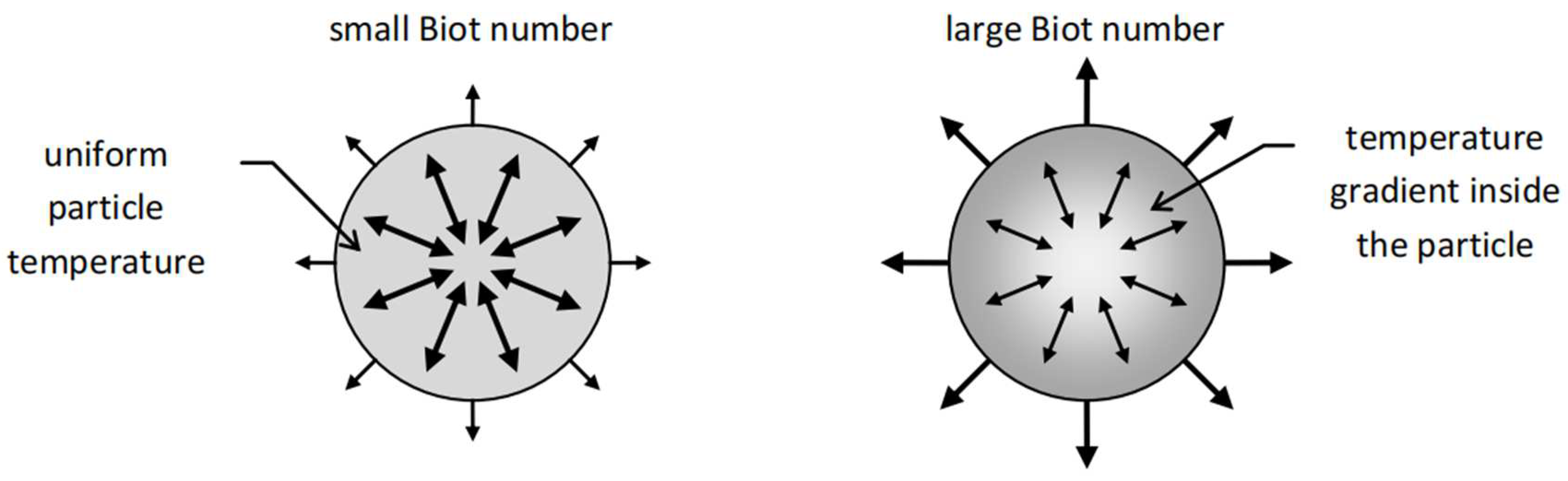
For a chosen solid with fixed thermal conductivity, the two ways to influence the Bi number are by changing the particle radius or changing $h_{fs}$ by varying the fluid velocity. A larger fluid velocity will decrease the thermal film thickness, leading to a decrease in the heat transfer coefficient, and therefore a larger Bi number. A larger particle size will similarly increase the Bi number.

Adding the solid conduction through the particle to the energy balance greatly increases the computational complexity of the simulation by adding an additional dimension in the $r$ direction. The solid conduction within the particle is then simply governed by the diffusion equation:

$$\frac{\partial T_s}{\partial t} = \frac{\partial}{\partial z}(k_s \frac{\partial T_s}{\partial z})$$

And is coupled to the fluid phase energy balance through appropriate boundary conditions. Practically, if the Bi number is < 0.1, we consider the solid to be thermally thin and a single temperature can be used to describe the solid.

There is a direct analogy for the mass transfer Biot number, $Bi_m$. Interestingly, in practical applications, it is the internal diffusion resistance that tends to dominate, as opposed to the film resistance for heat transfer.

In the last essay, I discussed the thermocline in packed bed thermal energy storage systems. From what we have seen so far, the selection of material for a packed-bed TES will strongly influence the Bi number. The Bi number is important as it has a strong effect on the performance of the thermocline.

For example, in the case of a large Bi number where thermal gradients persist in the particle, we are not utilising all of the thermal mass of the particle, and therefore, the amount of heat stored is reduced. In other words, the particles are not able to release all the energy fast enough, which also leads to a larger thermocline. Further to that, there are operational concerns as during the idle period, the temperature within the particle will equalise, reducing the overall temperature of the hot end or increasing the overall temperature of the cold end.

In the case of very small Bi numbers, the effective thermal conductivity through the bed becomes the dominant heat transfer mechanism and also increases thermocline thickness. A paper written by Hernandez-Jimenez, et al., 2025 suggests an optimal Bi number in the range of 0.1 to 1.5. The authors caviat that by saying this will depend on the exact system under analysis.