Velocity profile in a packed bed

Laminar flow within a pipe gives rise to the parabolic velocity profile:

$$u = U_0(1 - \frac{r^2}{R^2})$$

This parabolic velocity profile arises from the fluid's viscosity and the no-slip boundary condition at the wall, which together impose resistance to fluid motion. In contrast, a packed bed introduces additional resistance due to the presence of a porous medium. The resistance to flow depends on the local void fraction, which varies along the radius of the bed. This is best illustrated by thinking about the wall interface in contact with a single line of particles:

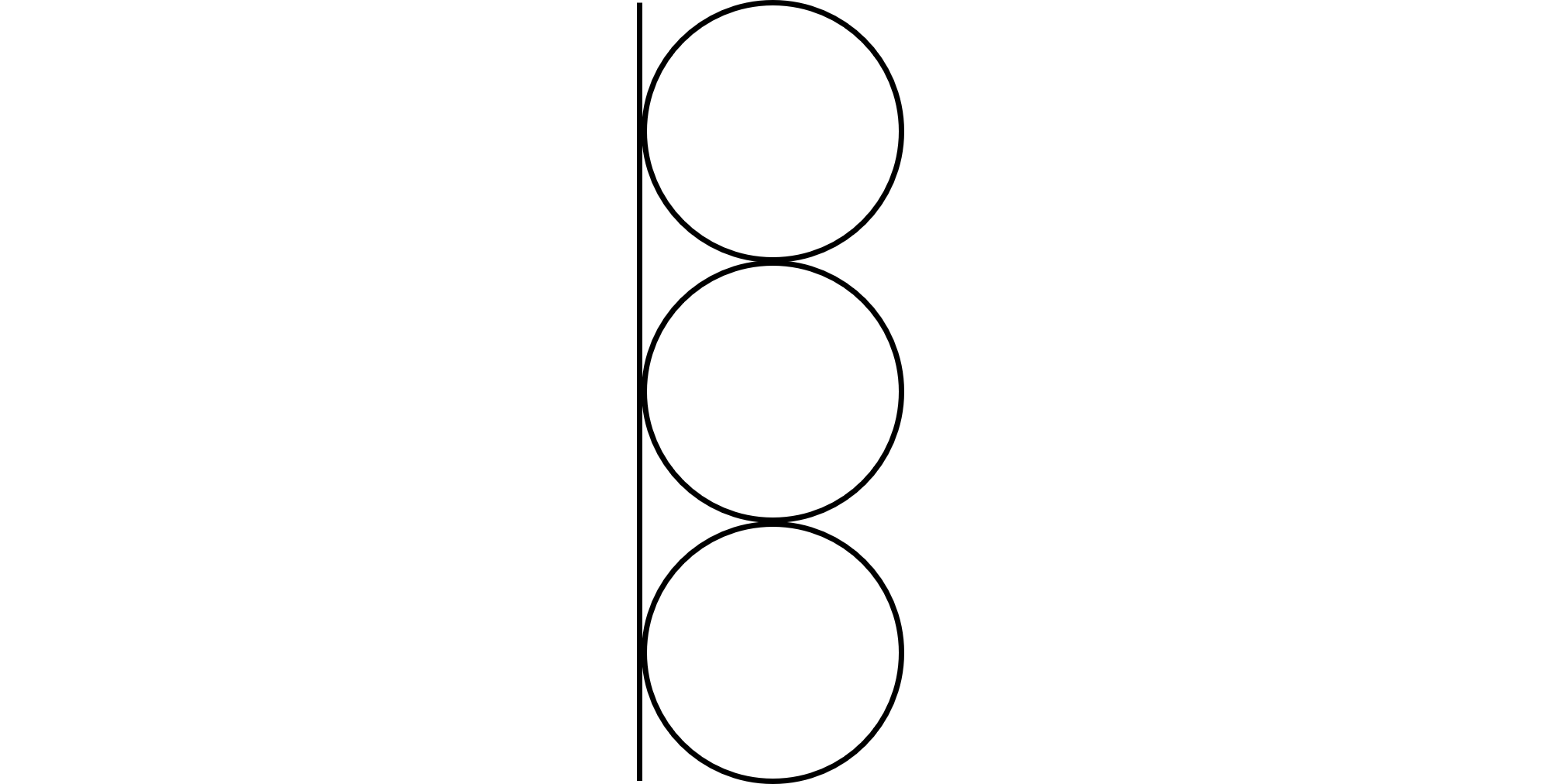
It's clear to see that at the interface, the void fraction $\epsilon_b = 1$. At a distance of one particle radius from the wall where the line of particles perfectly stacks, the void fraction is zero. Therefore, as the void fraction oscillates, so does the velocity:

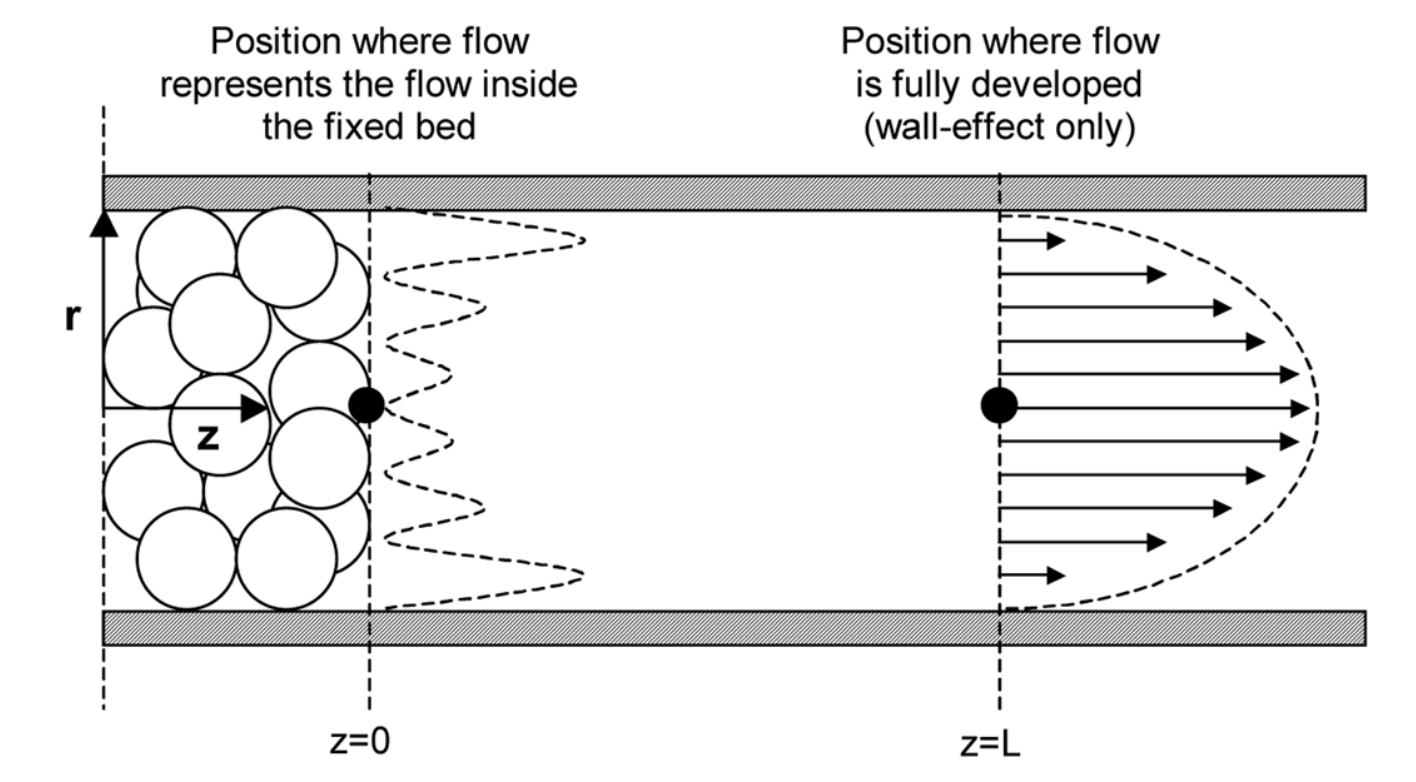
The larger $d_p/D$ is, the more this oscillation plays an important role in the fluid dynamics of the process. As an example, for adsorption breakthrough experiments in small laboratory setups where the column diameter is small, the large void fraction at the wall causes a phenomenon called "channelling". This is the process where fluid will move along the wall of the column much faster than the fluid in the center of the bed.

The implication here, when measuring the outlet concentration of a component, is that there will be premature breakthrough, impacting the shape of the breakthrough curve. Accounting for channelling in the modelling is extremely difficult, and it is usually desirable to design a better experiment.